waizui
A glimpse of quaternion
1. Definition of Quaternion
First, the definition of quaternion is:
\[\hat{q}=a+bi+cj+dk; \qquad (Equation 1) \\ \ \\ where \ (a,b,c,d \in R)\ and \ i^2=j^2=k^2=ijk=-1\]It looks very simple, and very similar to the definition of complex number, which is
\[w = a+bi \qquad (Equation 2) \\ \ \\ where \ (a,b, \in R)\ and \ i^2=-1\]In fact, there are some links between quaternions and complex numbers, and if you are interested in the history of quaternions and the inventor of it, check this wiki.
Quaternion is useful and compact in terms of representing three-dimensional rotation. So it’s widely used in various places.
In this article, only small fractions of quaternions will be discussed; Since the whole picture of quaternion is huge and lot of mathematical knowledge are required to be able to understand it.
2. Euler Transform
Let’s take a look at Euler Transform at first. To represent rotations, Euler Transform is an intuitive choice. It’s the multiplication of three matrices, each matrix is the rotation around it’s respective axis.
2.1 The head-pitch-roll transform
A commonly used view direction lies along the negative z-axis with the head oriented along the y-axis. shown in the figure.
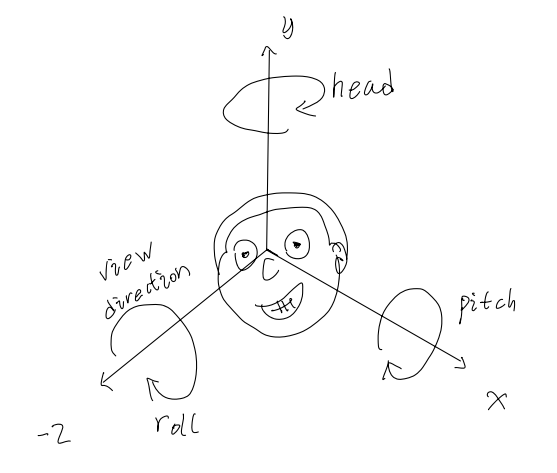
Rotations around y, x and z axis are called head, pitch, and roll.
More formally, the Euler Transform denoted E, is given by this equation:
\[E(h,p,r) = R_z(r)R_x(p)R_y(h) \qquad (Equation 3)\]where the h, p, r, are the Euler angles, representing in which order and how much the head, pitch, and roll should rotate around their respective axes.
2.2 Why not using Euler Transform
Despite of being intuitive and simple, Euler Transform has a fetal defect.
Since the last column and row of a pure rotation 4x4 matrix are zero, we can use a 3x3 matrix as the equivalent matrix, thus, Equation3 yields:
\[E(h,p,r) = R_z(r)R_x(p)R_y(h) \\ = \begin{bmatrix} cos\ r & -sin\ r & 0 \\ sin\ r & cos\ r & 0 \\ 0 & 0 & 1 \\ \end{bmatrix} \begin{bmatrix} 1 & 0 & 0 \\ 0 & cos\ p & -sin\ p \\ 0 & sin\ p & cos\ p \\ \end{bmatrix} \begin{bmatrix} cos\ h & 0 & sin\ h \\ 0 & 1 & 0 \\ -sin\ h & 0 & cos\ h \\ \end{bmatrix} \\ = \begin{bmatrix} cos\ r\ cos\ h -sin\ r\ sin\ p\ sin\ h & -sin\ r\ cos\ p & cos\ r\ sin\ h +sin\ r\ sin\ p\ cos\ h \\ sin\ r\ cos\ h +cos\ r\ sin\ p\ sin\ h & cos\ r\ cos\ p & sin\ r\ sin\ h -cos\ r\ sin\ p\ cos\ h \\ -cos\ p\ sin\ h & sin\ p & cos\ p\ cos\ h \\ \end{bmatrix} \\ (Equation 4)\]Ok, here comes one of the most funny things in computer graphics. If we let p=π/2, which means rotating around x axis 90 degrees and cos(p)=0, Equation4 will become:
\[\begin{bmatrix} cos\ r\ cos\ h -sin\ r\ sin\ h & 0 & cos\ r\ sin\ h +sin\ r\ cos\ h \\ sin\ r\ cos\ h +cos\ r\ sin\ h & 0 & sin\ r\ sin\ h -cos\ r\ cos\ h \\ 0 & 1 & 0 \\ \end{bmatrix}\]In this case, no matter what value we give r and h, the z coordinates of a vector to be rotated remains unchanged, which means one degree of freedom has lost, this is called gimbal lock. Because of the numerical instability, The Euler Transforms is not the ideal scheme of representing rotations.
3. Properties of Quaternion
Let’s get back to the Equation1,
\[\begin{align*} \because i\times j\times k &= -1 \\ \therefore (i\times j\times k)\times k &= -1\times k \\ (i\times j)\times(k\times k) &= -k \\ \because k^2 &= -1 \\ \therefore (i\times j)\times(-1) &= -k \\ -(i\times j) &= -k \\ i\times j &= k \end{align*}\]because of the same principle, the relation of ijk is:
\[ij=k\ \ ki=j \ \ jk=i \qquad (Equation5)\]which can be represented in the following figure.
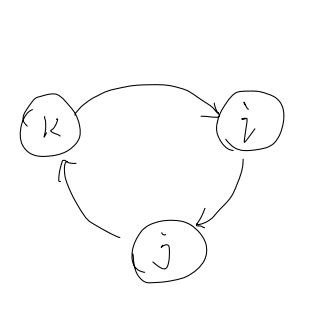
A quaternion can also be written in following way:
\[\hat{q} = (a,\vec{v}) \ ; \qquad a \in R \ \ and \ \ \vec{v} = bi+cj+dk \qquad (Equation6)\]where r is the real part, v is the imaginary part.
3.1 Addition
\[\hat{q_1} + \hat{q_2} = (a_1+a_2,\vec{v_1}+\vec{v_2})\]3.2 Multiplication
Note that the multiplication of quaternions is not commutative.
Giving quaternion q1 and q2, the multiplication of them is:
\[\begin{align*} &{\hat{q}}_1 {\hat{q}}_2 = (a_1,\vec{v_1})(a_2,\vec{v_2}) \\ &=(a_1+ib_1+jc_1+kd_1)(a_2+ib_2+jc_2+kd_2) \\ &=(a_1a_2-(b_1b_2+c_1c_2+d_1d_2)) \\ &+ i(a_1b_2+a_2b_1+c_1d_2-d_1c_2)\\ &+ j(a_1c_2+a_2c_1-b_1d_2+d_1b_2)\\ &+ k(a_1d_2+a_2d_1+b_1c_2-c_1b_2) \qquad (Equation7) \\ \end{align*}\]Since
\[\vec{v_1} \times \vec{v_2} = \begin{vmatrix} i & j & k \\ b_1 & c_1 & d_1 \\ b_2 & c_2 & d_2 \\ \end{vmatrix} = i(c_1d_2-d_1c_2) -j(b_1d_2-d_1b_2) +k(b_1c_2-c_1b_2)\]the product of two quaternions’ multiplication can also be written as
\[{\hat{q}}_1 {\hat{q}}_2 = (a_1a_2-\vec{v_1}\cdot\vec{v_2}\ , a_1\vec{v_2}+a_2\vec{v_1}+\vec{v_1} \times \vec{v_2}) \qquad (Equation8)\]the laws of multiplication are:
\[\begin{align*} &linearity: \qquad {\hat{q}}_3(s{\hat{q}}_1 + t{\hat{q}}_2) = s{\hat{q}}_3{\hat{q}}_1 + t{\hat{q}}_3{\hat{q}}_2; \quad (s{\hat{q}}_1 + t{\hat{q}}_2){\hat{q}}_3 = s{\hat{q}}_1{\hat{q}}_3 + t{\hat{q}}_2{\hat{q}}_3 \\ &associativity: \qquad {\hat{q}}_3({\hat{q}}_1 {\hat{q}}_2) = ({\hat{q}}_3{\hat{q}}_1) {\hat{q}}_2 \end{align*}\]3.3 Conjugate
\[\hat{q}^* = (a,\vec{v})^* =(a,-\vec{v}); \\ (\hat{q}^*)^* = \hat{q}; \\ ({\hat{q}}_1 + {\hat{q}}_2)^* = {\hat{q}}_1^* + {\hat{q}}_2^*; \\ ({\hat{q}}_1 {\hat{q}}_2)^* = {\hat{q}}_2^* {\hat{q}}_1^*; \\\]3.4 Norm
\[||\hat{q}|| = \sqrt{\hat{q} \hat{q}^*} = \sqrt{a^2+b^2+c^2+d^2}\]3.5 Inverse
The inverse of a quaternion is denoted by:
\[\hat{q}^{-1}\]the following equation defined the inverse of quaternion.
\[\hat{q}^{-1} \hat{q} = \hat{q} \hat{q}^{-1} = 1 \qquad (Equation9)\]We can derive the following formula by the norm definition:
\[\begin{align*} &||\hat{q}||^2 = \hat{q} \hat{q}^* \longrightarrow \frac{\hat{q} \hat{q}^*}{||\hat{q}||^2 } =1 \\ &(\hat{q}^{-1})\frac{\hat{q} \hat{q}^*}{||\hat{q}||^2 } =\hat{q}^{-1} \\ &\hat{q}^{-1} = \frac{ \hat{q}^*}{||\hat{q}||^2 } \qquad (Equation10) \end{align*}\]4. Quaternion and rotation
After knowing some basic properties of quaternion, let’s talk about the significancy of quaternions in terms of representing three-dimensional rotation.
4.1 Unit Quaternion
A unit quaternion is a quaternion whose norm equals to one, it also can be written in trigonometric form.
\[\hat{q} = (\cos{\phi},\sin{\phi}\ \vec{v}) = \cos{\phi}+\sin{\phi}\ \vec{v}; \qquad where \quad ||\vec{v}||=1; \quad \hat{q}^* = \hat{q}^{-1} \qquad (Equation11)\]4.2 Representing a rotation
Let’s say there is a unit quaternion q and a regular quaternion p. The components of p represent the four-dimensional coordinates of a vector(where the last component w is 1 or 0 for homogenous coordinates).
\[\hat{q} = (\cos{\phi},\sin{\phi}\vec{v}) \qquad \hat{p} = (w, xi+yj+zk )\]The rotation around axis v by the angle 2ϕ is:
\[\hat{p}' =\hat{q}\hat{p}\hat{q}^{-1} \quad or \quad \hat{p}' =\hat{q}\hat{p}\hat{q}^* \qquad (Equation12)\]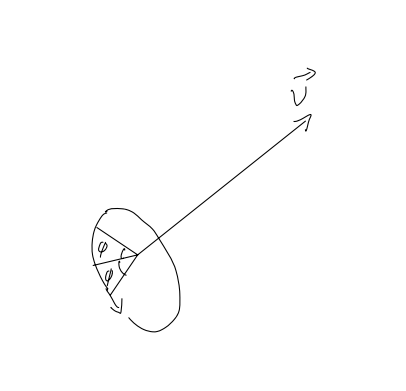
It’s very simple and compact. However the proof of Equation12 will not be discussed here, if you are interested, here are some resources will help to build a sense of how quaternion rotation work. A interactive explanation of quaternion, A detailed explanation of quaternion(In Chinese)
Besides, two rotations can be concatenated as following:
\[\begin{align*} \hat{p}'' &= \hat{q_1} \hat{p}' \hat{q_1}^{-1} \\ &= \hat{q_1} (\hat{q} \hat{p} \hat{q}^{-1}) \hat{q_1}^{-1} \\ &= (\hat{q_1} \hat{q}) \hat{p} (\hat{q}^{-1} \hat{q_1}^{-1}) \\ &= (\hat{q_1} \hat{q}) \hat{p} (\hat{q_1} \hat{q})^{-1} \\ &= (\hat{q_1} \hat{q}) \hat{p} (\hat{q_1} \hat{q})^{*} \qquad (Equation13) \end{align*}\]4.3 Matrix conversion
Reorganize Equation7 we can derive the equivalent matrix of left multiply a quaternion
\[\begin{align*} &{\hat{q}}_1 {\hat{q}}_2 = (a_1,\vec{v_1})(a_2,\vec{v_2}) \\ &=(a_1+ib_1+jc_1+kd_1)(a_2+ib_2+jc_2+kd_2) \\ &=(a_1a_2-(b_1b_2+c_1c_2+d_1d_2)) \\ &+ i(a_1b_2+a_2b_1+c_1d_2-d_1c_2)\\ &+ j(a_1c_2+a_2c_1-b_1d_2+d_1b_2)\\ &+ k(a_1d_2+a_2d_1+b_1c_2-c_1b_2) \\ &= \\ &(a_1a_2- b_1b_2- c_1c_2- d_1d_2)+ \\ &(b_1a_2+ a_1b_2- d_1c_2+ c_1d_2)i+ \\ &(c_1a_2+ d_1b_2+ a_1c_2- b_1d_2)j+\\ &(d_1a_2- c_1b_2+ b_1c_2+ a_1d_2)k\\ =&\begin{bmatrix} a_1& -b_1& -c_1& -d_1\\ b_1& +a_1& -d_1& +c_1\\ c_1& +d_1& +a_1& -b_1\\ d_1& -c_1& +b_1& +a_1 \end{bmatrix} \begin{bmatrix} a_2\\ b_2\\ c_2\\ d_2\\ \end{bmatrix} \qquad (Equation14) \end{align*}\]Therefor, left multiplying a unit quaternion q = a+bi+cj+dk, the equivalent matrix is:
\[M_{ql}= \begin{bmatrix} a& -b& -c& -d\\ b& a& -d& c\\ c& d& a& -b\\ d& -c& b& a \end{bmatrix} \qquad (Equation15)\]Based on same principle, the equivalent matrix of right multiply the conjugate of q is:
\[M_{q^*r}= \begin{bmatrix} a& b& c& d\\ -b& a& -d& c\\ -c& d& a& -b\\ -d& -c& b& a \end{bmatrix} \qquad (Equation16)\]Hence, a equivalent rotate matrix of q is:
\[\\ \begin{align*} M_q &= M_{ql}M_{q^*r} \\ &=\begin{bmatrix} 1& 0 & 0 & 0 \\ 0& 1-2(c^2+d^2) & 2(bc-ad) & 2(ac+bd) \\ 0& 2(bc+ad) & 1-2(b^2+d^2) & 2(cd-ab) \\ 0& 2(bd-ac) & 2(ab+cd) & 1-2(b^2+c^2) \\ \end{bmatrix} \qquad (Equation17) \\ \hat{q} \hat{p} \hat{q}^{*} &= M_q \hat{p}^T \\ \end{align*}\]Once a quaternion is constructed, compared to Equation4, the Euler Transform, no trigonometric calculation is needed, the equivalent matrix can be very efficiently deduced.
5. A Implement
…someday!
Now you can check a lua implementation of quaternion in this repository,
For example, the following code is multiplication of quaternions, check this repository for more details.
-- composing two quaterions by order a,b
---@param a Quaternion
---@param b Quaternion
---@return Quaternion
function Quaternion.__mul(a, b)
local r = a.r * b.r - (a.i * b.i + a.j * b.j + a.k * b.k) -- a1a2−(b1b2+c1c2+d1d2)
local i = a.r * b.i + b.r * a.i + a.j * b.k - a.k * b.j -- a1b2+a2b1+c1d2−d1c2
local j = a.r * b.j + b.r * a.j - a.i * b.k + a.k * b.i -- a1c2+a2c1−b1d2+d1b2
local k = a.r * b.k + b.r * a.k + a.i * b.j - a.j * b.i -- a1d2+a2d1+b1c2−c1b2
return Quaternion.new(r, i, j, k)
end
References
Real-Time rendering 4th edition